天体の位置計算では球面三角形の問題を解く場面があります。ここでは球面三角形の基礎的な法則を理解します。

球面三角形の正弦法則

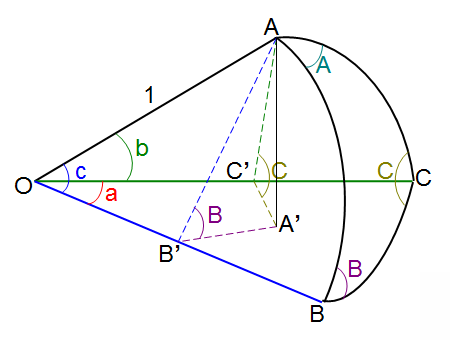
平面OBCを基準面とし、Aからこの基準面に垂線AA'をおろす。
A'からOBとOCに垂線A'B'とA'C'をひく。
すると、∠Bは∠AB'A'に等しく、∠Cは∠AC'A'に等しい。
球の半径(OA=OB=OC)を1とすると、OB'=cosc、OC'=cosbであり、
AB'=sinc、AC'=sinbである。すると、AA' = sincsinB = sinbsinCである。
これを書きかえると、sinb/sinB = sinc/sinCとなる。
これに輪環変換を行うと、sinc/sinC = sina/sinAとなる。
これらの関係をまとめると、以下の球面三角形の正弦法則が得られる。

球面三角形の余弦法則

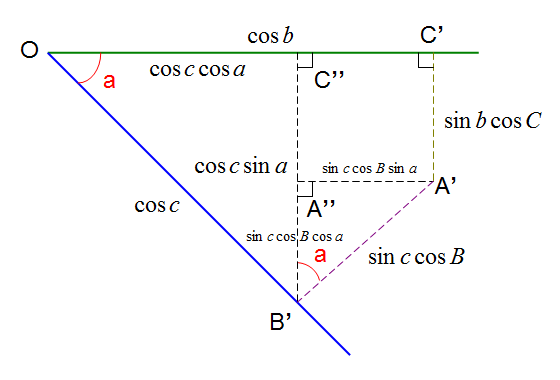
基準面上のOB'A'C'の関係は上図のようになる。
B'からOC'に垂線B'C''、そしてこの線にA'から垂線A'A''を引く。
すると、∠A'B'C''=aであるから、B'C''=coscsina、A'A''=sinccosBsinaとなり、
OC''=cosccosaとなる。(∠A'B'C''=90°-∠OB'C''=∠B'OC''=a)
OC'=OC''+C''C'=OC''+A''A'であるから、
cosb = cosccosa + sincsinacosB
これを書きかえると、
cosc = cosacosb + sinasinbcosC

これらの関係をまとめると、球面三角形の余弦法則が得られる。
また、A'C'=B'C''-B'A''=B'C''-B'A'cosaであるから、
sinbcosC = coscsina - sinccosacosB
sinccosA = cosasinb - sinacosbcosC

となり、二辺とその夾角から第三辺と他の一角を求める公式が得られる。

まとめ

• (1)より、sinasinB = sinbsinA
• (3)より、sinacosB = cosbsinc - sinbcosccosA
• (2)より、cosa = cosbcosc + sinbsinccosA

他の球面三角形

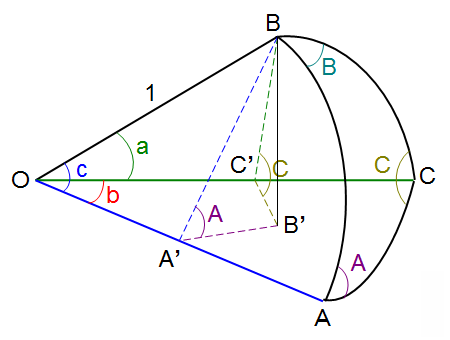
上図の球面三角形でも同様に上記の法則が成り立つ。