恒星時は天体を観測するために適した時刻系です。具体的には、恒星時と天体の赤経が等しい時、その天体は正中して観測に最適となります。ここでは、恒星時と太陽時の違いや恒星時を求める方法を理解します。

恒星時と太陽時

恒星時は恒星の日周運動に基づく時刻系です。 1恒星日は観測地の子午線を恒星が通過してから再び通過するまでに要する時間です。 1恒星日は約23時間56分4秒です。

太陽時は太陽の日周運動に基づく時刻系です。 1太陽日は観測地の子午線を太陽が通過してから再び通過するまでに要する時間です。 1太陽日は平均すると約24時間です。地球の公転周期は太陽年で約365.2422日です。

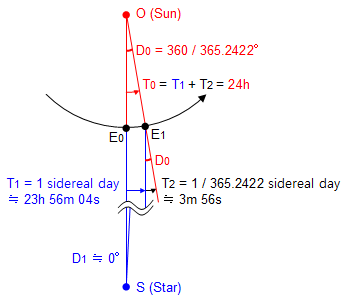
上図に示したように、太陽が南中してから翌日南中するまでの時間(1太陽日：T₀)と、太陽より遠方にある恒星が南中してから翌日南中するまでの時間(1恒星日：T₁)は異なり、 1太陽日は1恒星日より約4分(T₂)長いことがわかります。
T₂：地球が1日で公転する角度(360 / 365.2422 = 約0.9856°)の時間
T₂ = (0.9856 / 15) * 60 = 3.9424 = 約4分

恒星時を求める

恒星日をSD、地球の公転周期を365.2422日(太陽年)とすると、
(1 + 1 / 365.2422) * SD = 24 [時間]
(366.2422 / 365.2422) * SD = 24
SD = 24 * (365.2422 / 366.2422)
SD = 23.9344696 = 23h 56m 4.09s

上記より、恒星時間を求めると、
恒星時間 = (366.2422 / 365.2422) * 太陽時間
恒星時間 = 1.00273791 * 太陽時間
が成り立ちます。

したがって、世界時UTから恒星時θは下式で求めることができます。

θ = θ_G0 + 1.00273791 * UT + λ

θ_G0：0時UT1におけるグリニッジ恒星時
λ：観測地の経度(西経のとき負数)

また、恒星時θから世界時UTは下式で求めることができます。

1.00273791 * UT = θ - θ_G0 - λ
UT = (θ - θ_G0 - λ) / 1.00273791

UTが負数のときは24を加えて正数にします。

例題1

2000年1月1日0時(世界時)のグリニッジ恒星時が6h39m52.9sのとき、翌日0時(世界時)のグリニッジ天文台(東経0度)における恒星時を求め、前日0時(世界時)の恒星時間との差を求めてください。

(6 + 39 / 60 + 52.9 / 3600) + 1.00273791 * 24 - 0
= 6.664694 + 24.065710
= 30.730404
30.730404 - 24 = 6.730404
6.730404 - 6.664694 = 0.06571
0.06571 * 60 = 3.9426
0.9426 * 60 = 56.556
答：3m56.6s
この時間は地球が1日で公転する角度の時間と等しいことがわかります。
((360 / 365.2422) / 15) * 60 = 3.9426分

例題2

2000年1月1日12時0分0秒(日本標準時)のとき、東京都三鷹市の国立天文台(東経139度32分16.2秒)における恒星時を求めてください。ただし、2000年1月1日0時(世界時)のグリニッジ恒星時は6h39m52.9sとします。

日本標準時が昼12時のとき、世界時は夜明け前の3時(12時 - 9時)となるので、
(6 + 39 / 60 + 52.9 / 3600) + 1.00273791 * 3
+ (139 + 32 / 60 + 16.2 / 3600) / 15
= 6.664694 + 3.008214 + 9.302522
= 18.97543
0.97543 * 60 = 58.5258
0.5258 * 60 = 31.548
答：18h58m31.5s

グリニッジ恒星時を求める

1日の長さが年間を通じて変化しない平均太陽(mean solar)を仮定して、その太陽がイギリスにあるグリニッジ天文台の子午線上を通過する時角を、 グリニッジ恒星時 (Greenwich Sidereal Time : GST) と呼びます。

歳差運動を考慮した平均春分点に準拠する、世界時(UT1)0時におけるグリニッジ恒星時は下式で求めることができます。

T = 0.671262 + 1.00273791 * (世界時0時のユリウス通日 - 2440000.5)
θ_G0 = 24 * (T - [T])

[T]は、実数Tに対してT以下の最大の整数です。
例1：[135.79] = 135
例2：[-135.79] = -136

歳差運動を無視した2000.0分点に準拠する、
世界時(UT1)0時におけるグリニッジ恒星時は下式で求めることができます。

T = (世界時0時のユリウス通日 - 2451545.0) / 36525
T_G = (24110.54841 + 8640184.812866 * T + 0.093104 * T² - 0.0000062 * T³) / 86400
θ_G0 = 24 * (T_G - [T_G])

2000.0分点は2000年の年初における春分点のことです。(固定された標準分点)
[T_G]は、実数T_Gに対してT_G以下の最大の整数です。
例1：[135.79] = 135
例2：[-135.79] = -136

例題1

平均春分点に準拠するグリニッジ恒星時を用いて、2000年1月1日12時(世界時)のグリニッジ天文台(東経0度)における恒星時を求めてください。

2000年1月1日12時(世界時)のユリウス通日は2451545.0です。
T = 0.671262 + 1.00273791 * (2451545.0 - 2440000.5)
T = 0.671262 + 11576.107802
T = 11576.779064
θ_G0 = 24 * (11576.779064 - 11576)
θ_G0 = 24 * 0.779064
θ_G0 = 18.697536
0.697536 * 60 = 41.85216
0.85216 * 60 = 51.1296
答：18h41m51.1s

丁寧な手順を踏んだ以下の回答でも正解です。
2000年1月1日0時(世界時)のユリウス通日は2451544.5です。
T = 0.671262 + 1.00273791 * (2451544.5 - 2440000.5)
T = 0.671262 + 11575.606433
T = 11576.277695
θ_G0 = 24 * (11576.277695 - 11576)
θ_G0 = 24 * 0.277695
θ_G0 = 6.66468
θ = 6.66468 + 1.00273791 * 12 - 0
θ = 18.697535
0.697535 * 60 = 41.8521
0.8521 * 60 = 51.126
答：18h41m51.1s

例題2

2000.0分点に準拠するグリニッジ恒星時を用いて、2000年1月1日12時(世界時)のグリニッジ天文台(東経0度)における恒星時を求めてください。

2000年1月1日12時(世界時)のユリウス通日は2451545.0です。
T = (2451545.0 - 2451545.0) / 36525
T = 0
θ_G0 = (24110.54841 + 12 * 60 * 60) / 3600
θ_G0 = 18.697375
0.697375 * 60 = 41.8425
0.8425 * 60 = 50.55
答：18h41m50.6s

丁寧な手順を踏んだ以下の回答でも正解です。
2000年1月1日0時(世界時)のユリウス通日は2451544.5です。
T = (2451544.5 - 2451545.0) / 36525
T = -1.368925e-5
θ_G0 = (24110.54841 + 8640184.812866 * (-1.368925e-5)
+ 0.093104 * 1.873956e-10 - 0.0000062 * (-2.565305e-15)) / 3600
θ_G0 = (24110.54841 - 118.277650 + 1.744728e-11
+ 1.5904891e-20) / 3600
θ_G0 = 23992.270760 / 3600
θ_G0 = 6.664520
θ = 6.664520 + 1.00273791 * 12 - 0
θ = 18.697375
0.697375 * 60 = 41.8425
0.8425 * 60 = 50.55
答：18h41m50.6s

グリニッジ恒星時計算プログラム