赤道座標
赤道座標は天体の位置を表す天球座標系の一つです。 ここでは赤道座標の性質と地平座標から赤道座標を求める方法を理解します。
赤道座標の性質
赤道座標は2つの座標値で表されます。
- 赤経(α) または 時角(H)
- 赤緯(δ)
時角Hは観測地での地方恒星時θと天体の赤経αとの差で定義されます。
H = θ - α
H = 0 のとき、その天体は天球上の真南(子午線上)に位置します。
H = 6 のとき、その天体は天球上の真西に位置します。
H = 12 のとき、その天体は天球上の真北(子午線上)に位置します。
H = 18 のとき、その天体は天球上の真東に位置します。
子午線:地平線上の真北から天頂を通って真南へ至る天球上の仮想的な大円のこと。
この定義から赤経αは、地方恒星時θと時角Hとの差で計算できることもわかります。
α = θ - H
球面三角形の法則
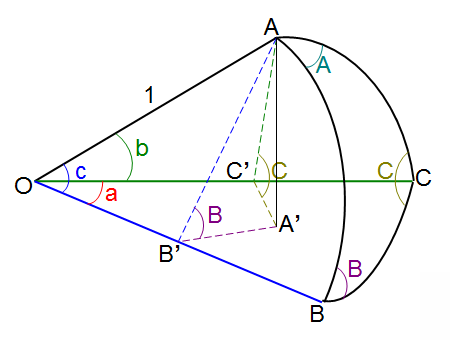
上図の球面三角形では球面三角法のページでまとめたように以下の法則が成り立ちます。
sinasinB = sinbsinA
sinacosB = cosbsinc - sinbcosccosA
cosa = cosbcosc + sinbsinccosA
sinacosB = cosbsinc - sinbcosccosA
cosa = cosbcosc + sinbsinccosA
この法則を用いて地平座標から赤道座標を求めます。
地平座標から赤道座標を求める
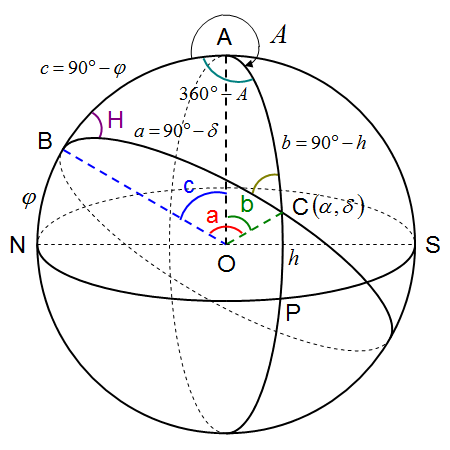
上図は球面三角形の法則で示した図を天球上に当てはめたものです。各記号の説明は以下の通りです。
| A | 天頂 |
| B | 天の北極 |
| C | 赤道座標を求める天体の位置 |
| a | 辺BCと等しい中心角:90° - δ |
| b | 辺ACと等しい中心角:90° - h (天頂距離) |
| c | 辺ABと等しい中心角:90° - φ |
| O | 観測地点 (天球の中心) |
| N | 真北 |
| S | 真南 |
| P | AとCを結ぶ大円が地平線と垂直に交わる点 |
| H | 天体の時角 |
| φ | 観測地の緯度 |
| A | 地平座標の方位角 |
| h | 地平座標の高度 |
| α | 赤道座標の赤経 |
| δ | 赤道座標の赤緯 |
球面三角形の法則より、
sin(90°-δ)sinH = sin(90°-h)sin(360°-A)
sin(90°-δ)cosH = cos(90°-h)sin(90°-φ) - sin(90°-h)cos(90°-φ)cos(360°-A)
cos(90°-δ) = cos(90°-h)cos(90°-φ) + sin(90°-h)sin(90°-φ)cos(360°-A)
sin(90°-δ)cosH = cos(90°-h)sin(90°-φ) - sin(90°-h)cos(90°-φ)cos(360°-A)
cos(90°-δ) = cos(90°-h)cos(90°-φ) + sin(90°-h)sin(90°-φ)cos(360°-A)
三角関数の余角公式より、
sin(90°-δ) = cosδ, cos(90°-δ) = sinδ
sin(90°-h) = cosh, cos(90°-h) = sinh
sin(90°-φ) = cosφ, cos(90°-φ) = sinφ
sin(90°-h) = cosh, cos(90°-h) = sinh
sin(90°-φ) = cosφ, cos(90°-φ) = sinφ
三角関数の補角公式より、
sin(360°-A) = -sinA
cos(360°-A) = cosA
cos(360°-A) = cosA
したがって、
cosδsinH = -coshsinA
cosδcosH = sinhcosφ - coshsinφcosA
sinδ = sinhsinφ + coshcosφcosA
cosδcosH = sinhcosφ - coshsinφcosA
sinδ = sinhsinφ + coshcosφcosA
これで、地平座標の方位角Aと高度hから、時角Hと赤緯δが求めることができます。